『STAOI』G - Round 3

A. 存在

题意：构造一个序列，使得任意一个子区间均存在主元素，且序列中元素的种类数最多（主元素指的是序列中出现次数大于等于序列长度一半的数）

构造题，由于是任意长度的子区间，首先从长度短的区间开始考虑。容易发现只要所有长度为奇数的区间合法，所有长度为偶数的区间自然合法，所以我们从长度为 $3$ 的区间开始考虑

考虑两个相邻的区间（如 $[1,3]$ 和 $[2,4]$），要想让这两个区间均存在主元素，$[1,4]$ 中必须得存在至少一对相邻且相同的数。由于在存在一对相邻且相同的数的情况下，后面放相同的数很明显是不优的，所以我们就必须得在间隔的位置再放一个和这对数相同的数，最后会发现我们能构造出来的最优的数列一定是长成类似这样的：$x,1,1,x,1,1,x,1,1,x,1,1...$，其中 $x$ 表示填任何数均可，把这样的数列输出即可，复杂度 $O(n)$

注：第一个数必须得是 $x$，因为 $1,1,x,1,1$ 并不和 $x,1,1,x,1$ 等价

B. Aulvwc

C. 高维立方体

题意：求解 $\sum\limits_{i=1}^n {\rm fib}(i)\left({\rm fib}^2(i)+{\rm fib}(i)+\sum\limits_{j=1}^{i-2} {\rm fib}^2(j)\right)$

结论题，对斐波那契数列存在如下规律：

$\sum\limits_{i=1}^n {\rm fib}(i)={\rm fib}(n){\rm fib}(n+1)$ $\sum\limits_{i=1}^n {\rm fib}^3(i)+{\rm fib}(i-2){\rm fib}(i-1){\rm fib}(i)={\rm fib}^2(n){\rm fib}(n+1)$

具体的理解可以用这张图的二维和三维模式理解 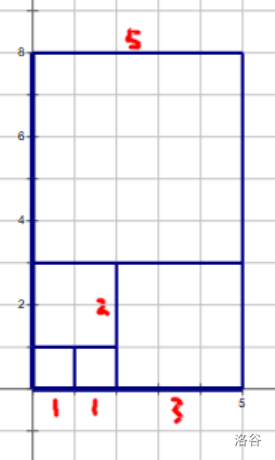最后用矩阵快速幂求解即可，复杂度 $O(\log n)$

D. 大豆

题意：$k$ 次操作，每次从左往右遍历 $n$，$b_n \leftarrow \sum\limits_{i=2}^n b_{\lfloor\frac ni\rfloor}$，求最终 $b_m$ 的大小

考虑暴力，很容易发现是一个类似杜教筛的数论分块，所以直接做就可以做到 $O(n^\frac 34)$ 的复杂度，但是仍然不够，于是考虑比 $O(n\sqrt n)$ 更优的预处理方法

首先假设操作前的序列为 $a$，将 $b_i$ 的转移表达式写出来，可以得到 $b_n=a_n-\sum\limits_{i=2}^n b_{\lfloor\frac ni\rfloor}$。我们发现这个式子和杜教筛很像，而杜教筛筛的前缀和一般都有 $O(n\ln n)$ 复杂度的算法，所以我们考虑将这个式子拆回杜教筛转化之前的式子，于是就可以得到 $f_i=\Delta b_i, g_i=1,h_i=\Delta a_i$，于是原式就可以转化为 $f * g = f * 1 = h$，两边同时卷上 $\mu$ 即可得到 $f=\mu * h$，即 $\Delta b_n=\sum\limits_{d \vert n} \mu(\frac nd)\Delta a_i$，所以我们可以直接对原式做 Dirichlet 卷积就可以预处理出前 $B$ 个的答案，最终复杂度 $O(B\ln B+\frac n{\sqrt B})$，在 $B=n^\frac 23$ 时可以取到一个较优的复杂度，可以通过（可能需要卡常，比如 $\mu(x)$ 不直接乘改成 if-else 之类的）