2023“钉耙编程”中国大学生算法设计超级联赛（2）

~~感觉我遇到了卡时间 + 卡空间 + 找规律的三重暴击，已寄~~

1001. Alice Game

题意：二人博弈，每次可以消掉一个完整的长度 $\leq K$ 的区间 $\sf or$ 一个长度为 $K$ 的子区间并将原来的区间分为两个分离的完整区间，要求不能操作的人输，求是否先手必胜

博弈论，优先打表，发现当 $n {\ \rm mod\ } (4K+2) = K+1$ 时先手必胜，直接 $O(1)$ 计算即可，复杂度 $O(T)$ ~~本来想说看看题解怎么说，结果发现题解也是打表，就呵呵了。。。~~

1002. Binary Number

题意：给定一个 01 序列，一次操作为选定一个区间翻转 01 状态，求操作恰好 $k$ 次后能得到的 01 序列对应的最大的二进制数

签到题，分类讨论当 $n=1$ 时，输入为 $1$，输出为 $\lnot (k {\ \rm xor\ } 1)$ 当 $n>1$ 时，分两种情况： - 若 $k \leq$ 零的连续段个数，则尽量翻即可 - 若 $k>$ 零的连续段个数，则可以通过反转 $01$ 为 $10$ 再翻成 $11$ 把多余的操作数消耗掉（多 $2$ 步及以上的可以直接重复翻同一个区间使多的步数变为 $0$ 或 $1$）

注意特殊情况（$s=11...11, k=1$）此时 $s_n=11...10$，复杂度 $O(1)$

1003. Counter Strike

1004. Card Game

题意：汉诺塔的魔改版本，要求每堆的盘子的大小必须是连续的，求在有 $n$ 根柱子的时候最多能够将多少个盘子从第一个柱子移到最后一个柱子

大胆猜测 $ans=2^{n-1}-1$，直接通过 - 以下是正解：

令 $f(n)$ 为有个牌堆时的最大移牌数，为了方便表述，我们认为 $f(1)=0$。很显然 $f(2)=1$。当 $n>2$ 时，我们先移动点数最大的牌堆，此时除了终点牌堆外其余牌堆都有牌且点数小于当前堆的任意一张牌，因此这些牌堆又不可以使用，这一步可以移动 $f(1)+1$ 张牌，其中的加1含义是移动牌堆底部的最大牌；随后我们移动点数第二大的牌堆，由于上一步操作，我们获得了一个空牌堆，这个空牌堆是可以借用的，所以这一步可以移动 $f(2)+1$ 张牌，以此类推。故而 $f(n)=\sum\limits_{i=1}^{n-1}f(i)+1$，展开得 $f(n)=2^{n-1}-1$

1005. Or

1006. Fencing the cows

一句话题意：有 $n$ 个黑点和 $m$ 个红点，用最少的黑点围住所有的红点

点不好找，我们考虑找边注意到要围上所有的红点，所有红点必须在黑边的一侧，而所有的黑边首位相连最后会构成一个环，而找出最少的点构成的多边形本质上就是求最小环的长度所以我们可以根据可能构成结果多边形的两个点建边，在建成的图上用 Floyd 跑最小环即可，复杂度 $O(n^2m+n^3)$

1007. foreverlasting and fried-chicken

题意：求给定无向图中与下图同构的子图的数量

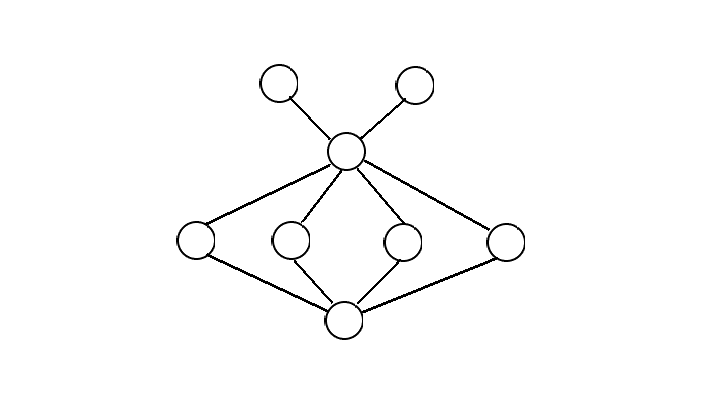
考虑枚举目标子图中度数为 $6$ 和 $4$ 的两个点，则包含这两个点构成的子图数为 $\binom{cnt}4\binom{deg_u-4}2$，其中 $cnt$ 为 $u$ 与 $v$ 之间长度为 $2$ 的路径个数。故答案为 $\sum\limits_{u=1}^n\sum\limits_{v=1}^n \binom{cnt}4\binom{deg_u-4}2[u \neq v]$，其中 $deg_u$ 直接在加边时记录即可，$cnt$ 可以使用 bitset 优化，最终复杂度为 $O(\frac{n^3}w)$，可以通过 ~~题解居然用了循环展开，我。。。~~

1008. Hello World 3 Pro Max

题意：给定一个字符串，要求维护一个数据结构，支持单点修改字符和区间查询 $helloworld$ 的子序列个数

不考虑修改，很容易发现一个很单纯的 dp： $dp_{i,j}$ 表示匹配到 $i$ 匹配长度为 $j$ 的子序列个数，则 $dp_{i,j}=dp_{i-1,j}+p_{c_j}*dp_{i-1,j-1}$ 加入修改，则可直接改为矩阵 dp $+$ 线段树维护即可，复杂度 $O(11^3(n+q\log n))$ ~~然后就是万众期待的卡常环节~~ 出题人给出了三种卡常方法： 1. 上三角所以可以让 $k$ 从 $i$ 开始到 $j$ 结束，$j$ 从 $i$ 开始到 $10$ 结束 2. 取模很慢可以改为 unsigned long long 最后统一取模 3. 循环展开 ~~（感觉这个出题人是真的喜欢循环展开，已经是一套题里的第二个了。。。）~~

总之经过一顿卡常，这道题就能过了 ~~（没错，这就是正解）~~ ~~（不得不说这个出题人是真心喜欢卡常。。。）~~ ~~（不排除可能是 hdu 太慢了的过）~~

1009. String Problem

题意：给定一个字符串，求解 $\sum\limits_{i=1}^K len(s_i)-K$，其中 $s_i$ 是满足含有至多一个字母的原串的所有回文子串

签到，尽可能的划分为一个字母的长段，每一段对结果贡献为 $len-1$，直接求和即可，复杂度 $O(\sum n)$

1010. Klee likes making friends

题意：给定一个长度为 $n$ 的序列，每个点有一个代价，一个序列的代价是其中所有点的代价和，要求选出一个子序列，满足代价最小，并且原序列中每相邻 $m$ 个数中至少有两个数是这个子序列中的数

考虑定义 dp 状态 $dp_{i,j}$ 表示前 $i$ 个中最后一个选了的为 $i$，倒数第二个选了的为 $j$ 时的最小代价，则 $dp_{i,j}=\min\limits_{i-k+1 \leq m} dp_{j,k}+a_i$ 直接暴力 $dp$ 时间复杂度是 $O(n^3)$，注意到所有的 $k$ 构成一个以 $j$ 为端点的连续段，于是可以把 $i,j$ 的枚举顺序交换，那就可以用滑动窗口记录最小值，从而将一维枚举优化掉，复杂度 $O(n^2)$ 然后你可能认为你能过了，于是尝试交了一发，发现。。。它 MLE 了仔细观察数据范围，发现 $n \leq 2e4$，而空间范围只有 $64\sf\ MB$，很明显是不够用的，所以考虑优化空间 ~~（我发现这个出题人真的很喜欢恶心人，卡了时间还不够还要来卡我空间。。。）~~ 再仔细观察数据范围，可以发现 $m \leq 2e3$，比 $n$ 少了一个数量级，所以只需要将 dp 的两维优化到 $O(m)$ 本题就可以通过了对于第二维而言，我们很容易发现两维数之间的差是 $\leq m$ 的，所以可以用两维数之间的差代替第二维，复杂度优化为 $O(m)$ 对于第一维，由于每次更新一行的值只需要前面 $m$ 行的内容，所以可以把第一维直接模个 $m$ 用滚动数组压掉即可，复杂度 $O(m)$ 最终复杂度优化为 $O(Tm^2)$，可以通过

1011. SPY finding NPY

题意：求最小的 $k$ 满足所有的排列中第 $k+1 \sim n$ 个数中第一个 $>$ 前 $k$ 个数的最大值的数是 $n$ 的数量最多

刚开始我想着要枚举最大值，后来发现其实不需要那么麻烦设 $p_{n,k}$ 表示长度为 $n$ 的数列选取前 $k$ 个作为参考时选出 $n$ 的概率，则 $p_{n,k}=\frac 1n\sum\limits_{i=k+1}^n\frac k{i-1}$（$i$ 枚举的是 $n$ 在排列中所在的位置，$\frac k{i-1}$ 表示的是当 $n$ 在 $i$ 时，前 $i-1$ 个数的最大值在 $1 \sim k$ 之间的概率）所以只需要提前预处理出 $\frac 1i$ 的前缀和，到时候直接一个个查就可以了，复杂度 $O(Tn)$ ~~（幸好这个题不卡精度，要不然我觉得出题人可以成为一代宗师了。。。）~~ 更进一步，其实可以发现 $p_{n,k} \approx \frac kn\int_k^{n-1}\frac 1x{\rm d}x=\frac kn\ln\frac{n-1}k$，是个单调递增函数，于是可以三分求解，复杂度 $O(T\log n)$ 再进一步，可以直接将原式近似为 $\frac kn\ln\frac nk$ 后求导得 $k=\frac ne$ 时最大，由于左右可能有误差，所以只要左右枚举一下就能求出最后的结果，复杂度 $O(T\alpha)$

1012. Coin

题意：有 $n$ 个人，其中有 $K$ 个人是同伴，给出 $M$ 次操作，每次操作会选出 $2$ 个人，要求他们一个人给另一个人一个硬币，或者什么都不做，过程中每个人手中的硬币数不能超过 $a_i$，求 $K$ 个人在经历所有操作之后能得到的数的最小值

考虑网络流，以每个人手中的硬币作为流动物，每个人是一条流量为 $a_i$ 的主管道，每次在一个时刻可以交换硬币的两个人之间加上一个容量为 $1$ 的管道，所有人从源点获得 $1$ 的流量，最终能流到汇点的是那 $K$ 个同伴，那么这个网络的最大流就是

这样建图是 $O(nm)$ 的，考虑简化。很明显每个人有用的点只有㓟交换的时候，别的时候的管道都是一条直线，没有分叉，所以只在发生交换的时候新建节点，点数就可以从 $O(nm)$ 降为 $O(n+m)$，可以通过